問題16
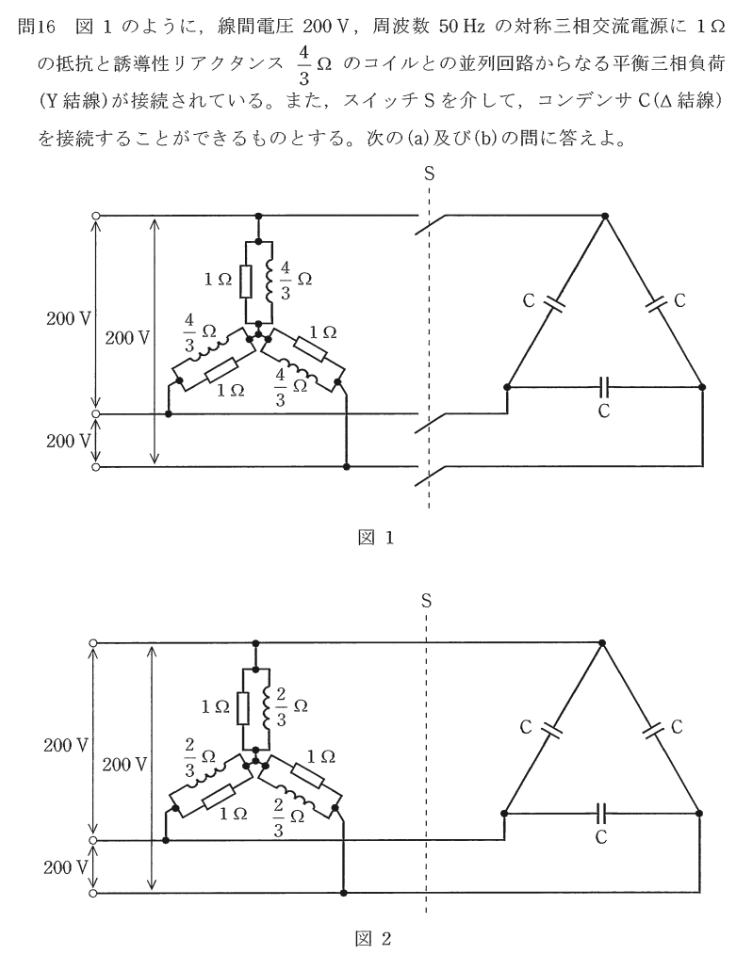

a) 相電圧をV(V)とすると、V=200/√3(V)
抵抗R(Ω)に流れる電流をIr(A)とすると. Ir=V/R=200/√3x1(A)
三相分の有効電力をP(kW)とすると、
P = 3x(Ir)²xR =3x(200/√3x1)²x1=40000=40(kW)
誘導リアクタンスX〈Ω)に流れる電流をIx(A)とすると、X=4/3(Ω)として、
Ix=V/X=200/√3x4/3 (A)
三相分の無効電力をQ(kvar)とすると、
Q = 3x(x)²xX =3x(200/√3x4/3)²x4/3=30000=30(kvar)
b) 負荷の誘導リアクタンスが4/3(Ω)→2/3(Ω)に変化(減少)しているので、誘導リアクタンスに流れる電流は倍増する。この増加した電流分を進相をとるコンデンサで吸収すると、負荷の無効電力は変化しないことになります。
変更前の負荷の無効電流:Ix=V/X=200/√3x4/3 =150/√3 (A)
変更後の負荷の無効電流:Ix’=V/X=200/√3x2/3 =300/√3 (A)
コンデンサで吸収する無効電流:Ic =Ix’-Ix =150/√3 (A)
負荷の接続と同じようにコンデンサの接続をΔからYに変換すると1相分のコンデンサ容量は3倍即ち、3Cになるから、Icは次式で表されます。
Ic = V/Xc = 200/√3 x ω3C = 150/√3
電源数fは50(Hz)、ω=2πf であるから、上式よりコンデンサ容量C(μF)は次の様になります。
C = 5/20ω= 5/20×2πx50=1/40π=800(μF)
コメント 計算そのものは割と単純ですが。コンデンサの接続のΔ→Y変換でCが3Cになることが
分からないと間違るので要注意です。
問題17
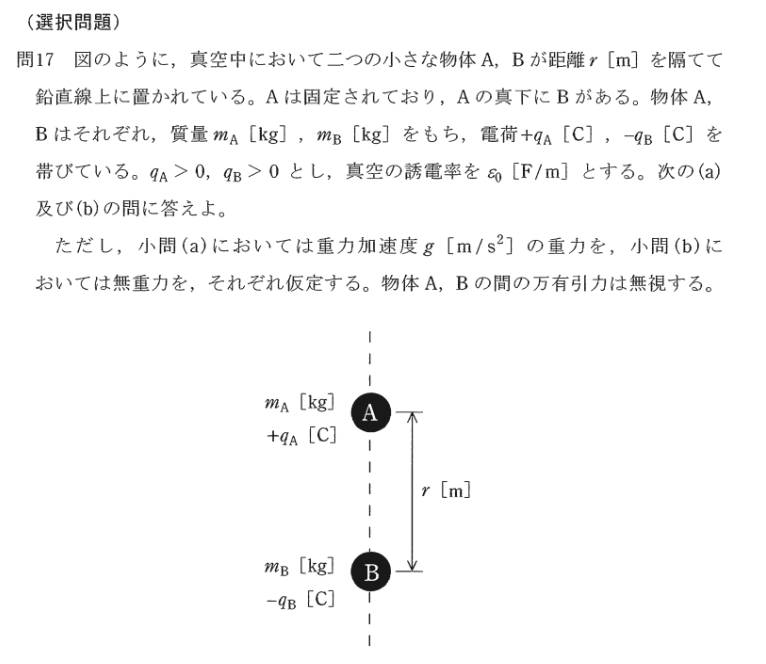

a) A,B間にはクーロン力が働き、Bには重力が働く(Aにも重力は働くがAは固定でありのでAは不動)
Bが上方のAに近づくのは、A,B間のクーロン力(この場合吸引力)がBに作用する重力より勝っているからです。
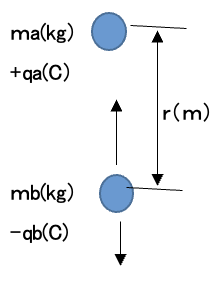
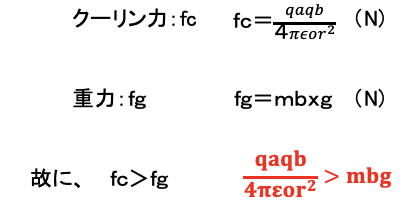
b) 無重力であるので、Bには重力の加速度は作用しない。Bを速度vbで放ったとき、Bの運動エネルギーをWb(J)とすると、Wb = 1/2 x mbxVb² (J) 物体Bに作用する物体Aからの静電エネルギーをUb(J)とすると、Aの電位をVaとして、
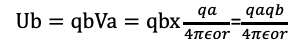
Wb >Ub の時、物体Bは物体Aからの吸引力から脱出して、下降するがWb<Ubになると、Aからの吸引力が勝って下降から上昇に転換します。よって
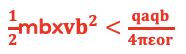
となります。
スキマ時間も有効活用できるオンライン講座問題18
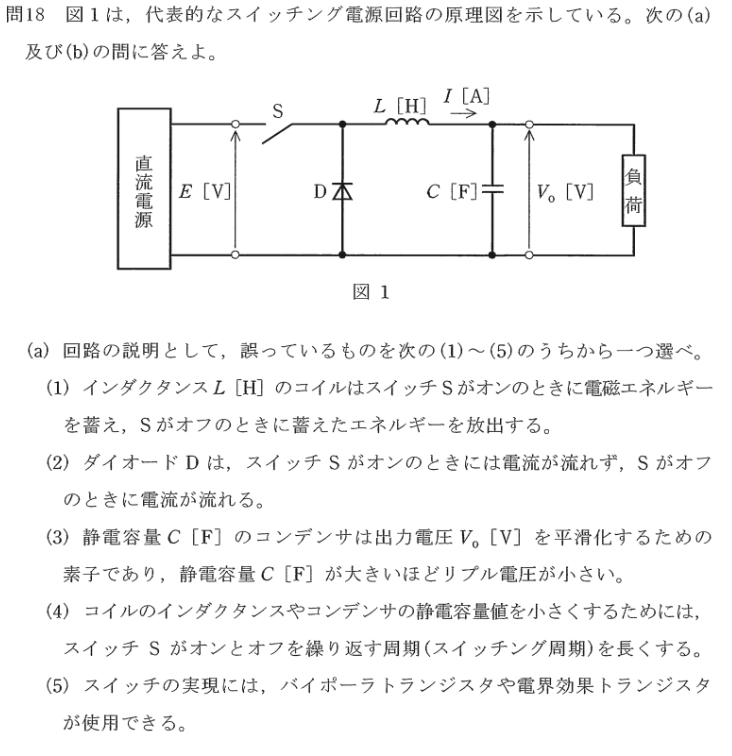
a) 記述式問題
- インダクタンスL(H)のコイルはスイッチSがオンの時に電磁エネルギーを蓄えSがオフの時に蓄えエネルギーを放出する。 記述通り。
- ダイオードDはスイッチSがオンの時には電流が流れず、Sがオフの時に電流が流れる。 記述通り。
- 静電容量C(F)のコンデンサは出力電圧Vo(V)の平滑化するための素子であり、静電容量C(F)が大きい程リプル電圧は小さい。 記述通り。
- コイルのインダクタンスやコンデンサの静電容量値を小さくするにはスイッチSがオンとオフを繰り返す周期(スイッチング周期)を長くする。 誤り。 →スイッチング周期を短くする。
- スイッチの実現には、ハイホーラトランジスタや電界効果トランジスタが使用できる。記述通り。
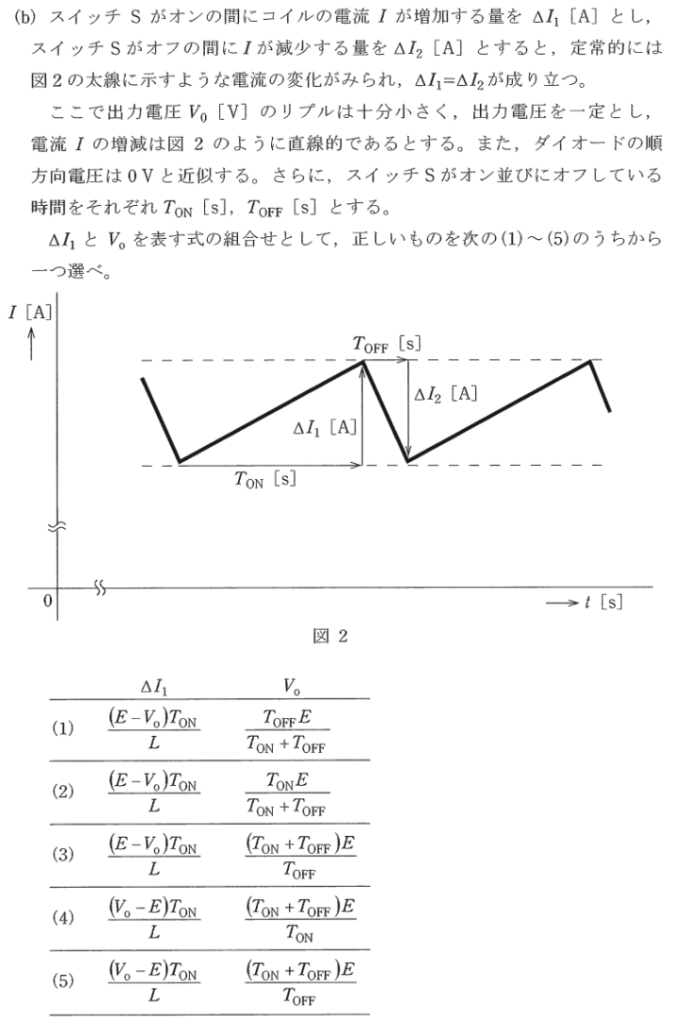
b)
ΔI1を表す式について:電流は電圧を抵抗で割ったもの、電圧の値はE>Voであり、抵抗分に相当するのはインダクタンスLであろので、 ΔI1を表す式は (E-Vo)Ton/Lです。
Voを表す式について:VoはEの%ED(1周期中のONする割合)であるので、 Vo=ExTon/(Ton+Toff) です。



コメント