問題13
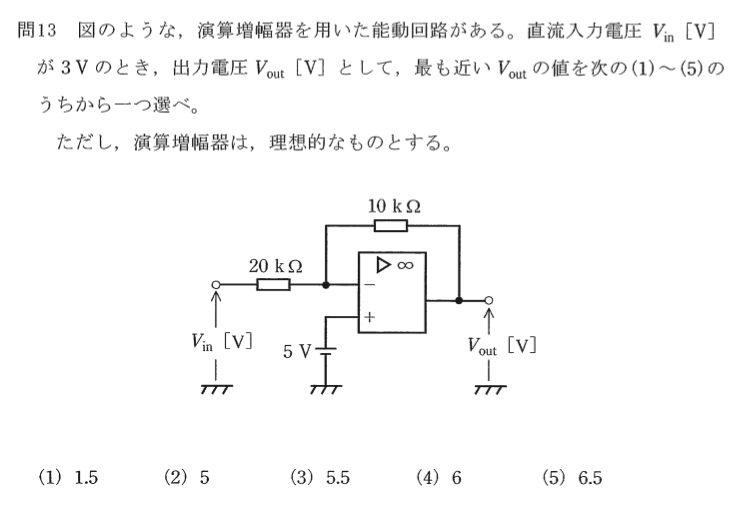
演算増幅器は理想的なものとすると、(-)の端子電圧は5(V)、負荷電流をI(A)とすると、次式が成り立ちます。
Vin(V) + 20(kΩ)xI(A)=5(V)
5(V) + 10(kΩ)xI(A)=Vout(V)
この両式から電流I(A)を消去すると、Vin=3(V)であるから、
Vout(V) = 5 + 10×2/20 = 5 + 1 =6(V) 正解→(4)
コメント
理想的な増幅器ではバーシャルジョイントで(-)端子にバイアス電圧(ここでは5V)が掛かるとして、回路の電圧関係式を立てて解くようにしてください。
問題14
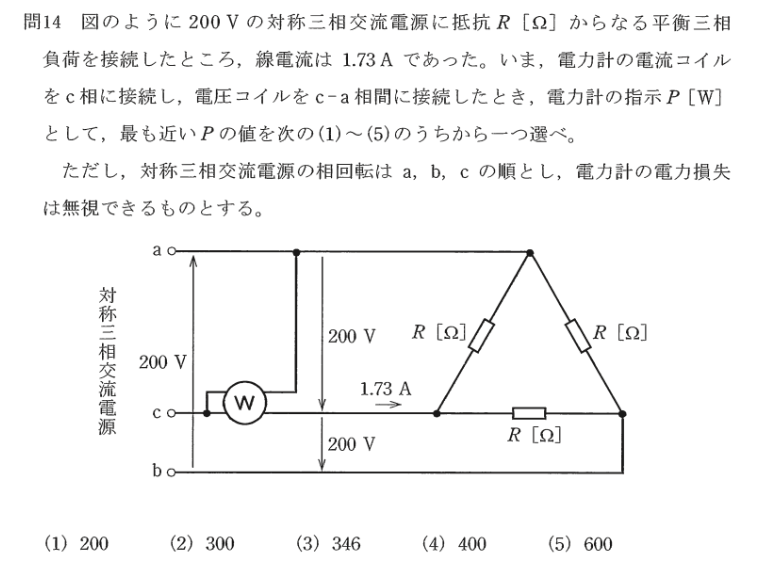
回路は抵抗負荷の平衡三相3線式回路であるから、線間電圧Vと線電流Iが分かっているので、三相電力Po(W)は
上記の回路の電力計の接続は2電力計法による三相電力の測定法の電力計の片方の接続であるので、電力計の指示Pを2倍した値が三相電力Po=600(W)になります。
故に、 2P=600(W) より P=300(W) 正解→(2)
コメント
- 三相電力の測定で2電力計法を知っているとすぐ解ける問題です。
- 2電力法忘れいても、線間電圧と線電流の位相差は30°であることを理解していると、P=200x1.73xcos30°=200x1.73x√3/2=300(W)と計算できます。
問題15
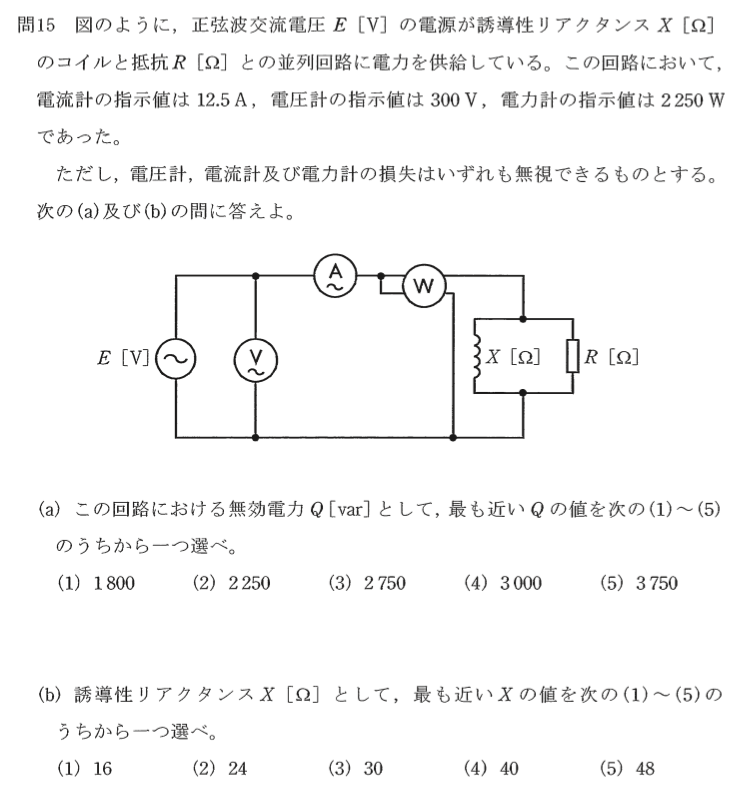
- A:電量計の指示: 12.5(A)
- E:電圧計の指示: 300(V)
- W:電力計の指示: 2250(W)
(a): 無効電力Q(var)はいくらか?
皮相電力をS(VA)とすると、 S=ExA=300x12.5=3750(VA)
力率cosθは cosθ=W/S=2250/3750=0.6
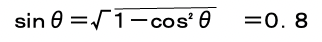
無効電力Qは Q=Sxsinθ=3750x0.8=3000(var)
解答→(4)
(b): 誘導リアクタンスX〈Ω)はいくらか。
抵抗R(Ω)は R = E²/W= 300²/2250 = 40(Ω)
電流を抵抗に流れる電流Irとリアクタンスに流れるIxに分けると、 Ir = 300/40 = 7.5(A)
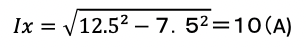
よって X=300/10=30(Ω) 正解→(3)
コメント
① (a)は皮相電力、有効電力、無効電力、力率の相互関係の問題です。CosとSinの相互変換を使うと、ピタゴラスの定理を使うより計算が楽になります。
② (b)は誘導リアクタンスXの値を求める計算ですが、負荷が並列回路の場合には電流から計算した方が容易です。




コメント