問題5
(解答)
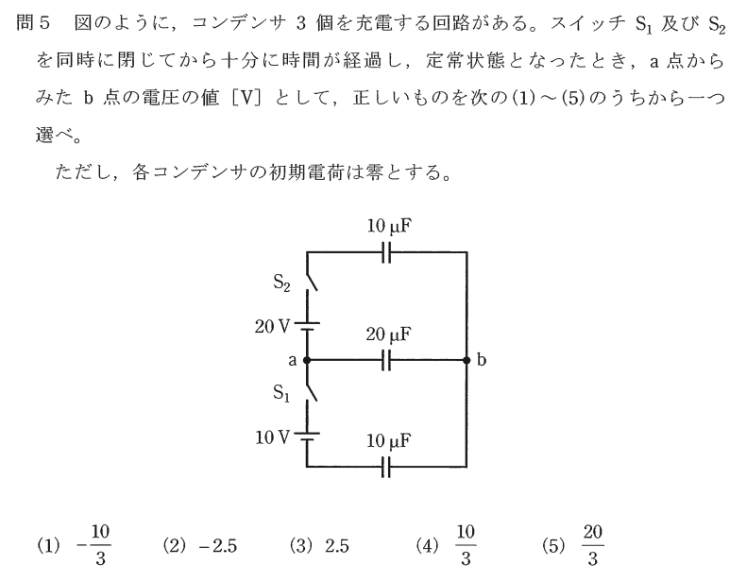
コンデンサ3個を充電した場合のコンデンサのab間端子電圧の計算
先ず、各部の電圧、静電容量、電荷を下図のようにきめます。この場合、b側はa側より電圧が高いと仮定して、各コンデンサの電荷の正負(+、-)は図示のようにします。また、電圧の極性は、負(-)から正(+)を正、コンデンサの極性も同様に負(-)から正(+)を正とします。
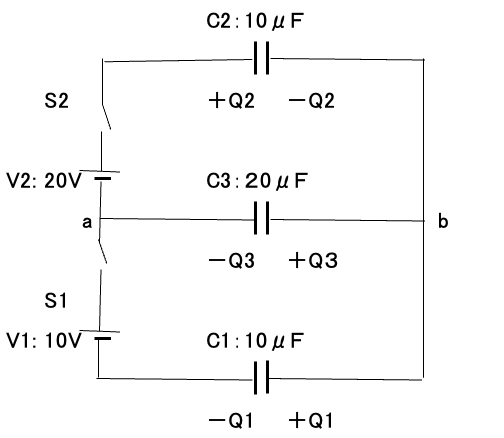
初期条件で各コンデンサーには電荷は零(0)であったので、電荷保存の法則から、次式が成り立ちます。
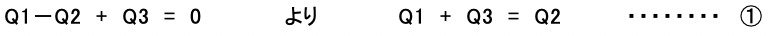
次に、キルヒホッフの第二法則(任意の閉回路に於いて、閉回路にそった電位の変化の和は零(0)である。)を適用すると、次式の関係が成り立ちます。
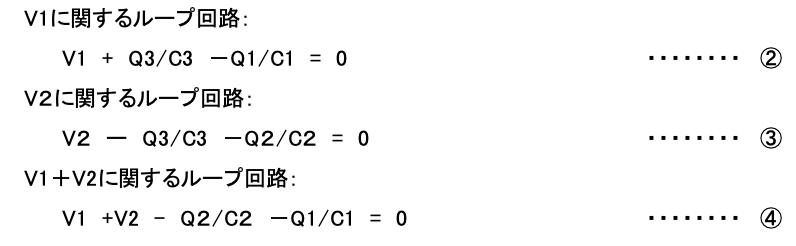
①~④ 式に於いて、 V1=10(V) V2=20(V) C1=C2=10(μF) C3=20(μF)として、代入して整理すると
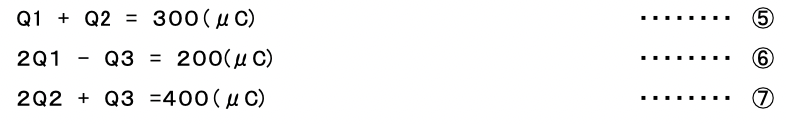
①式および⑤~⑦の関係から、連立方程式を解いて(途中は省略)

故に、a,点から見たb点の電圧をVab(V)とすれば、
Vab = Q3/C3 = 50/20 = 2.5(V) 正解→(3)
(コメント)
- 静電容量に関する基本的な問題であるが、計算のプロセスが多いので割と手間が掛かり、間違いやすい問題です。
- 電荷の極性(+、-)と初期条件(最初の電荷は零)とキルヒホッフの第二法則の理解が大切です。
問題6
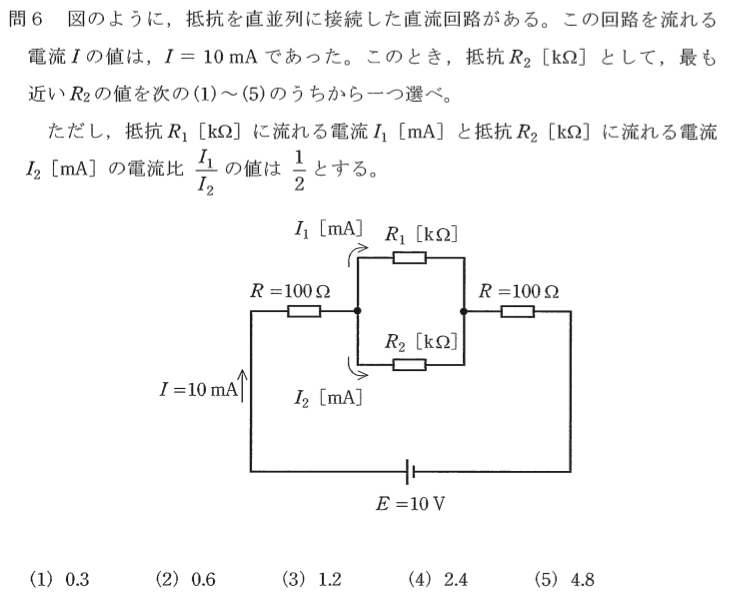
図の回路において、 題意より、I1/I2=1/2 であるので、抵抗R1とR2の比はR1:R2=2:1 、即ち、 R1=2xR2 であることが分かります。
全抵抗をR0とすれば、 Ro=E/I=10(V)/(mA)=1000(Ω) です。
R1とR2の合成抵抗を、R12とすれば、
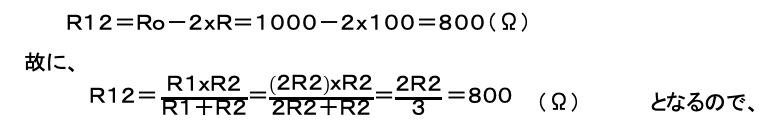
R2=800x3/2=1200(Ω)=1.2(kΩ) 正解→(3)
(コメント)
この問題では、 I1:I2=1:2 なら、 R1:R2=2:1 であることに気付くことが大切です。
問題7
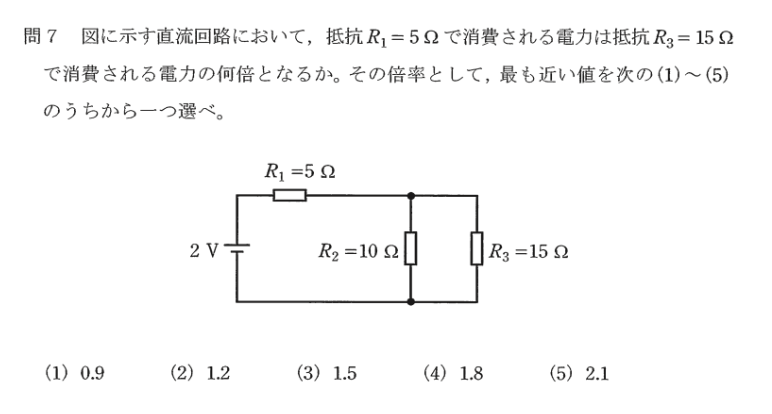
先ず、全抵抗Ro(Ω)をもとめ次に、R1を流れる電流I1(A)を求める。
Ro=R1+R2xR3/(R2+R3)=5+10x15/(10+15)=5+6=11(Ω)
I1 = E/Ro = 2/11(A)
抵抗R2とR3に電流をI2,I3とすれば、抵抗R2,R3の逆比でI1が分流するから、
I3=I1xR2/(R2+R3)=I1x10/(10+15)=I1x2/5=4/55 (A)
R1の消費電力をP1(W)、R3の消費電力をP3(W)とすれば、
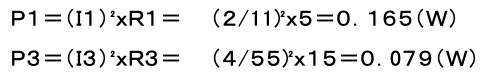
故に、 P1/P3=0.165(W)/0.079(W) = 2.1 正解→(5)
問題8
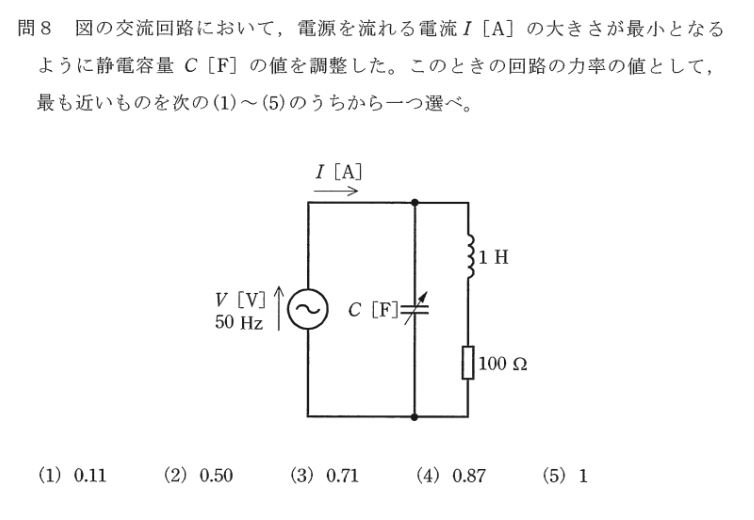
コンデンサCの値を調整して電源を流れる電流I(A)を最小にする問題、即ち、負荷の力率改善の基本問題です。負荷電流Io(A),コンデンサCに流れる電流をIⅽとして、電源電圧Vを基準にベクトル図を描くと、下図のようになります。 ここで、Ir と Iℓは負荷電流の有効分と無効分、θは負荷インピーダンス角です。
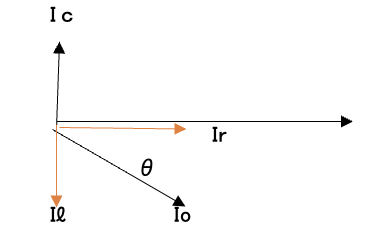
力率改善は、負荷に並列にコンデンサーと接続することによって、無効電流Iℓを相殺するようにIⅽを流すようにして、負荷力率を改善する方法です。故に、Iℓ=Iⅽになるようにコンデンサの値を調整するれば電流Iが最小になり、この時、電流と電圧は同位相となり力率は1である。




コメント